Task:
You can try to sign messages and send them to the server, 52.0.217.48 port 60231. Sign the right message and you\'ll get the flag! Only problem---you don\'t have the signing key. I will give you this, though: sigs.txt is a file containing a bunch of signatures. I hope it helps. (P.S. Don\'t try and send the exact signatures in that file---that\'s cheating!)
Given archieve attached below.
Solution:
Let's start! Unpack archieve and take a look inside. We have three python scripts and one .txt file. Two python files contain only constants, but last contains server implemetation. Let's have a closer look on it:
def handle(self):
self.captcha()
sig = self.request.recv(5000)
sig = json.loads(sig)
if "r" not in sig or "s" not in sig or "m" not in sig:
self.request.close()
return
r = sig["r"]
s = sig["s"]
m = sig["m"]
if not elgamal_verify(r, s, m):
self.request.close()
elif is_duplicate(sig):
self.request.close()
elif m != "There is no need to be upset":
self.request.close()
else:
self.request.sendall(FLAG)
self.request.close()And:
def elgamal_verify(r, s, m):
if r <= 0 or r >= SAFEPRIME:
return False
if s <= 0 or s >= SAFEPRIME-1:
return False
h = int(hashlib.sha384(m).hexdigest(), 16)
left = pow(GENERATOR, h, SAFEPRIME)
right = (pow(PUBKEY, r, SAFEPRIME) * pow(r, s, SAFEPRIME)) % SAFEPRIME
return left == right
DUPLICATES = []
def is_duplicate(s):
return s in DUPLICATESSo, wha is happening here? First step is Anti-captcha (proof of work) - you have to proove, that you are robot (cos human cant calculate hash in mind...=) ), you can bypass it with bruteforce, using scripts from previos arcticles.
On the second step server checks signature: it takes from user json with m, r and s fields and perfoms some checks:
- (r,s) signature is valid for message m
- Message and it's signature were not used before (not in given sigs.txt file)
- Message m is equal to "There is no need to be upset"
So we just have to forge valid signature for meddage: "There is no need to be upset".
Because verification function is called "elgamal_verify", you may suppose that server uses ElGamal Scheme. Let's open wikipedia and gain some information about this scheme. Among all you can find "Security" part and some interesting things in it:
The signer must be careful to choose a different k uniformly at random for each signature and to be certain that k, or even partial information about k, is not leaked. Otherwise, an attacker may be able to deduce the secret key x with reduced difficulty, perhaps enough to allow a practical attack. In particular, if two messages are sent using the same value of k and the same key, then an attacker can compute x directly.
And we have we have sigs.txt file with several signatures.. looks like we are on the right way... but what is k? Wiki says:
To sign a message m the signer performs the following steps.
- Choose a random k such that 1 < k < p − 1 and gcd(k, p − 1) = 1.
- Compute
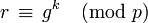 .
. - Compute
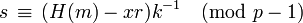 .
. - If
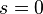 start over again.
start over again.
Then the pair (r,s) is the digital signature of m. The signer repeats these steps for every signature.
So, if in two signatures same k was used, both signatures have same r. Let's examine given sigs.txt file to find out same r values. For example, this script will do it for you:
import re
with open('sigs.txt', 'r') as f:
data = f.read()
searcher = re.compile( "\"r\": \d+")
r_vals = searcher.findall(data)
uniq = []
for r in r_vals:
if r in uniq:
print r
else:
uniq.append(r)Result:
"r": 24030551483122053624716977527407536977518653033297939409122802809740309624953770247347499500115945237454766787108175375302146086541500888306491588588147326149187734156069939639058405265571675349658277792098286622286226058008567542381029931604553716421740469902946532483973532336362867141732245398972208695076558639383660148089152829691282160772599817042880415931978266720626748559045779449893737272112671672750802677804265935211941474277988895796905249955578045776622418603597677320454557350772863501720544466286669388103247173728880382526588182905215363298438385070158385795742683303408289812120424459186306607441289 "r": 15596574224423604337174975776788465266479462558269645435687330615427783442319450174310669167504694165949734195772140468403401519160093357880254143018633950179114008556651092403391366077557363361555123124177670387232880718011385652224689886844787549431939261644192798219757366042713163922831165605478332687249430607990154018556718572496906645239311390495141354282987806832079357224945158666328969818853986069540836255016227603632402476397515152119360294922495895244235309968400537736534622122663697025389872185310053285819453794953849878570802282548259719716065417998189738453640724390984216257023730024188208988434794 "r": 7642569978590436429035839941747247560961995622187738908962159214058334385040541356267957242899354560757177741259486145756635387643986997662432251492305334195580243624629435620896520306233592274992724847384959546615834897272240261629833454725467996866722488751905291163060514410309569216190018941208834286631363010818364154295177563417071850364776094073956065971376816168479731258230097121738745272755290500815682780120887578487480236247646661452058929568790006839190000789494099743010979644184683260698667768183665065310183202237640230653237055185353887233368385521231171006737686056695974479215510810069532170450224 [Finished in 0.1s]
We find three r, which are not unique. So we can perform attack, that was described above. Wiki says:
s = ( H(m) - xr )k-1 (mod p-1)
sk = H(m) - xr (mod p-1)
H(m) = sk + xr (mod p-1)
We have two different messages with two signatures (s,r), where s are different but r are equal. So we have system of two equations:
H(m1) = s1k + xr (mod p-1)
H(m2) = s2k + xr (mod p-1)
Where x and k is unknow variables. Be careful, when solving this system, because integers modulo p-1 is a ring, so not all elements have multiplicative inverse. For example, even s wouldn't has it.
You can use any Math application to solve system of equations by modulo and find k and x. I've used Wolfram Math:
Solve[
15596574224423604337174975776788465266479462558269645435687330615427783442319450174310669167504694165949734195772140468403401519160093357880254143018633950179114008556651092403391366077557363361555123124177670387232880718011385652224689886844787549431939261644192798219757366042713163922831165605478332687249430607990154018556718572496906645239311390495141354282987806832079357224945158666328969818853986069540836255016227603632402476397515152119360294922495895244235309968400537736534622122663697025389872185310053285819453794953849878570802282548259719716065417998189738453640724390984216257023730024188208988434794*x +
20193160426525825914749944534502183854793246273057225225204130786954179606391520252397561856344584750457489718289118609515303464507510251417077403315954173676057341891301159286752647600395198190644724307893515345893595410667424425312908674343690968733843740920409803587443515922925501638028491932183400780974410265039483539351372898810463837406346416273301833999371981123383744331959625540606861187311099827640470542835373136973637049034852358457864170556183428016586548277807973991611705101720973851865311156212618466002189499709957796272187041939722207610584175170433726950035007314375587759506260786928657084551208*y ==
17522164631796177405895087447911918224805069054544219936136496691782804368700681944248318092297704863697843193489206 &&
15596574224423604337174975776788465266479462558269645435687330615427783442319450174310669167504694165949734195772140468403401519160093357880254143018633950179114008556651092403391366077557363361555123124177670387232880718011385652224689886844787549431939261644192798219757366042713163922831165605478332687249430607990154018556718572496906645239311390495141354282987806832079357224945158666328969818853986069540836255016227603632402476397515152119360294922495895244235309968400537736534622122663697025389872185310053285819453794953849878570802282548259719716065417998189738453640724390984216257023730024188208988434794*x +
20950544720225190240516588643124156640166137751307772794120839122642879744566309989204234525193060193095734419581892490241084064977398989989423034374978973475972879096343609617333859217032402467474794063367359126064209414247112196692749986283927599483857635906461630946699655333336064650658571060838418022831773012112148484373450539087980144060939705883970226872558602362137321434221468807558634789744082687788692428002582578979320390623784385653753663765668912704533244714593744067390408848738952250051111603136134591670549919971405683223154547996667007410471545395238084694224087888217638321220704877088996234667758*y ==
32912878155772232082988690525300428836530642510373329387039819701838393571941848326053069623907005119234663553785330,
{x, y},
Modulus ->
27327395392065156535295708986786204851079528837723780510136102615658941290873291366333982291142196119880072569148310240613294525601423086385684539987530041685746722802143397156977196536022078345249162977312837555444840885304704497622243160036344118163834102383664729922544598824748665205987742128842266020644318535398158529231670365533130718559364239513376190580331938323739895791648429804489417000105677817248741446184689828512402512984453866089594767267742663452532505964888865617589849683809416805726974349474427978691740833753326962760114744967093652541808999389773346317294473742439510326811300031080582618145726]And result is:
Answer:
{{x -> 11405148977472070847365218710766449078537570969688340378848352437920775589263471165689667400222906768815975260917123165802980646318353389631475775638254459726964055271804077962848769755220905417865830271596783314761387652548615547386856401898810558155866110142664500325585994569852700494187601969524512877504501310480889704990280605643619505056187819289992366250062643439920600261106116347627717948112330653523084554538170888898127933270176684391756706118533788708485259278763353731318153045165374215647633533950855383457673005747323515328227853308910032144312613158202921709938645864922336849172162584600594548383769 +
13663697696032578267647854493393102425539764418861890255068051307829470645436645683166991145571098059940036284574155120306647262800711543192842269993765020842873361401071698578488598268011039172624581488656418777722420442652352248811121580018172059081917051191832364961272299412374332602993871064421133010322159267699079264615835182766565359279682119756688095290165969161869947895824214902244708500052838908624370723092344914256201256492226933044797383633871331726266252982444432808794924841904708402863487174737213989345870416876663481380057372483546826270904499694886673158647236871219755163405650015540291309072863 C[1],
y -> 12780654076712315342557968007566379935229954276230807639665702142103549136408699104332337502550652581806514878279261654171262095484373525061520969023188821681199026858966468950451221700940218653506601368343894689092533052209732513940302093154785769183690626111706770904919054659023003137158039635431673035380262813165085357833180324316706979051198536038699978511970853276885780181015508612084020605897756865495255350696748220033237316185373458895608809435734616059720556237199048361906711902462009427742458373806078932083281313989085236666731027152436636238565509653859120339870549660036293474217320107816478127848604 +
13663697696032578267647854493393102425539764418861890255068051307829470645436645683166991145571098059940036284574155120306647262800711543192842269993765020842873361401071698578488598268011039172624581488656418777722420442652352248811121580018172059081917051191832364961272299412374332602993871064421133010322159267699079264615835182766565359279682119756688095290165969161869947895824214902244708500052838908624370723092344914256201256492226933044797383633871331726266252982444432808794924841904708402863487174737213989345870416876663481380057372483546826270904499694886673158647236871219755163405650015540291309072863 C[2]}}
As you can see, system has muliply solutiuons.
You can very fast check all four combinations by forging four variants of (s,r) signature for m = "There is no need to be upset", and sending it on server. If you use same r as in sigs.txt, you just need to compute s, so:
K = 12780654076712315342557968007566379935229954276230807639665702142103549136408699104332337502550652581806514878279261654171262095484373525061520969023188821681199026858966468950451221700940218653506601368343894689092533052209732513940302093154785769183690626111706770904919054659023003137158039635431673035380262813165085357833180324316706979051198536038699978511970853276885780181015508612084020605897756865495255350696748220033237316185373458895608809435734616059720556237199048361906711902462009427742458373806078932083281313989085236666731027152436636238565509653859120339870549660036293474217320107816478127848604 + 13663697696032578267647854493393102425539764418861890255068051307829470645436645683166991145571098059940036284574155120306647262800711543192842269993765020842873361401071698578488598268011039172624581488656418777722420442652352248811121580018172059081917051191832364961272299412374332602993871064421133010322159267699079264615835182766565359279682119756688095290165969161869947895824214902244708500052838908624370723092344914256201256492226933044797383633871331726266252982444432808794924841904708402863487174737213989345870416876663481380057372483546826270904499694886673158647236871219755163405650015540291309072863
R = 15596574224423604337174975776788465266479462558269645435687330615427783442319450174310669167504694165949734195772140468403401519160093357880254143018633950179114008556651092403391366077557363361555123124177670387232880718011385652224689886844787549431939261644192798219757366042713163922831165605478332687249430607990154018556718572496906645239311390495141354282987806832079357224945158666328969818853986069540836255016227603632402476397515152119360294922495895244235309968400537736534622122663697025389872185310053285819453794953849878570802282548259719716065417998189738453640724390984216257023730024188208988434794
Kinv = inverse(K, M)
print Kinv
11229564743034185040004960050772054007682662152342489588663134546157830837439948644777566056798431052050328871856833998547970536669342678490701009207205388039479343267225423580587116767573396520467953567708885431696965609591547186713704202330941400518771586809861731353532477280946818593198085158822727812249062666604332954171368291583140313845753585453894318934470456670469827222218354006201600442374222432023493236612146637469249317961367788649325550166802023675758482489748891700581825892091702679217253672563341697873025935541062804335772599169547952882534586596303285146433449671309000641194778425709515061034061L
H = int(hashlib.sha384("There is no need to be upset").hexdigest(), 16)
X = 11405148977472070847365218710766449078537570969688340378848352437920775589263471165689667400222906768815975260917123165802980646318353389631475775638254459726964055271804077962848769755220905417865830271596783314761387652548615547386856401898810558155866110142664500325585994569852700494187601969524512877504501310480889704990280605643619505056187819289992366250062643439920600261106116347627717948112330653523084554538170888898127933270176684391756706118533788708485259278763353731318153045165374215647633533950855383457673005747323515328227853308910032144312613158202921709938645864922336849172162584600594548383769 + 13663697696032578267647854493393102425539764418861890255068051307829470645436645683166991145571098059940036284574155120306647262800711543192842269993765020842873361401071698578488598268011039172624581488656418777722420442652352248811121580018172059081917051191832364961272299412374332602993871064421133010322159267699079264615835182766565359279682119756688095290165969161869947895824214902244708500052838908624370723092344914256201256492226933044797383633871331726266252982444432808794924841904708402863487174737213989345870416876663481380057372483546826270904499694886673158647236871219755163405650015540291309072863
S = ((H - X * R) * Kinv) % M
print S
11057062360037254017289635018921773984183564064092395096838773711381090984064311698289768170915721461871937003117929770925039756903570621025707383705465627567970676462056327449577227456755524929286234463839696828725619393734746030826431182855696671016288244742041130665258517881078515879578523743937721290168743838774382061947237978837869517592441458667243091811392910778481879611111807313162640186698122857701857400429810865528683646940672873418762238830032505222891402579366927300508292794863485872865578871520392827529932070319462416460050694529429370692076137317134639455980792967653965353227009612149885652150641LSend (r,s,m) json and get:
nonces_are_fucking_rad_amirite
Flag: nonces_are_fucking_rad_amirite
